In D&D games, players often roll 1d20 + modifiers vs a difficulty check (DC) given by the DM. When not specified, the DM chooses a challenge level guided by the table below.
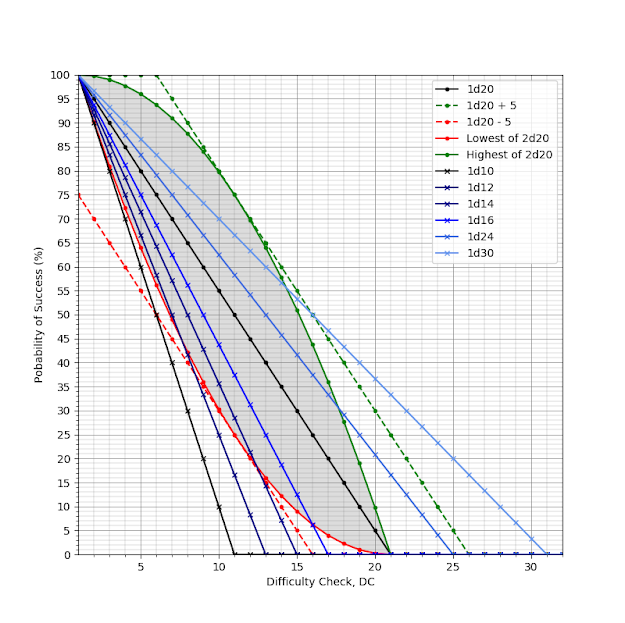
With DCC's dice chain rule for checks, the probability of success barely changes for low DCs, but it changes widely for higher DCs, as the maximum value of the die check changes above and below 20. It means that a character in advantage has the chance of succeeding for DCs that were normally impossible, whereas it makes it impossible to succeed vs some high DCs. Strategically, this makes advantage and disadvantage much more important in game. The players gain a lot, if they are creative for gaining advantage in combat and skill checks. If they are smart, they will try to figure out strategies to convince the DM to give them more advantage.
| DC | Challenge Level | Success Probability of Unmodified Roll |
| 5 | Easy | 80 % |
| 10 | Normal | 55 % |
| 15 | Hard | 30 % |
| 20 | Very Hard | 5 % |
| 25 | A Hero's Work | 0 % |
| 30 | Nearly Impossible | 0 % |
Rolling a single die produces an uniform probability distribution function, where each face has the same probability to show up. Since it is a d20 being rolled, each side has 1/20 = 0.05 = 5 % chance of showing up. Since we are interested in the probability of all success values, we sum the probability of each value on the side of success. In mathematical terms, this is the cumulative distribution of the die probability integrated from right to left, instead of the traditional left to right, because we are integrating the higher or equal than the DC, instead of lower than the DC. Graphically, this inversely integrated cumulative distribution function is seen below.
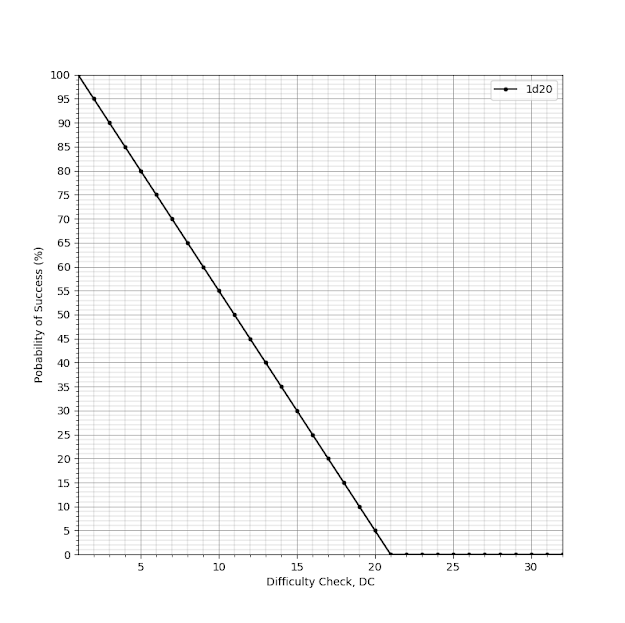 |
| Figure 1: Probability of success when rolling a plain 1d20 vs a DC. |
Adding Modifiers
When modified, the probability of success goes up 5% by each modifier (i.e., +5% for +1, and -5% for -1). |
| Figure 2: Probability of success when rolling 1d20 + mod vs a DC. |
Advantage and Disadvantage in 5e
D&D 5e introduced the advantage and disadvantage mechanics, where 2d20 are rolled and the highest or the lowest value are used, respectively. This is a neat way of expressing advantage and disadvantage, because it increases the chances of success or failure, and the DM doesn't have to decide how much is the advantage and disadvantage in terms of +/- modifier. Besides, more dice, more fun! However, the probability of success is not linear anymore.
In case of the advantage roll, success is obtained when you don't fail in any of the two dice:
\[ P_\text{adv} = 1 - P(d20 < DC)^2 = 1 - [1 - P(d20 \geq DC)]^2 \]
In case of the disadvantage roll, success is obtained when you succeed in both rolls:
\[ P_\text{dis} = P(d20 \geq DC)^2 \]
Interestingly, this coincides with modifying the roll by +/-5 for DC = 11. However, for all other cases, it is worse than giving a bonus of +5 for advantage, and it is better than giving a penalty of -5. Advantage highly increases the chance of success of DC < 11, but doesn't increase the chance of success of DC > 11 as much. Disadvantage does the opposite, it increases the chances of failure of higher DCs a lot, but decreases less the chance of failure of lower DCs. Moreover, 5e's advantage and disadvantage rule keeps the roll result bound to the 1-to-20 range, whereas modifying the roll shifts the roll result to values outside that range.
Advantage and Disadvantage in DCC
Dungeon Crawl Classics (DCC) is D&D system forked from D&D 3.5e. DCC uses non-conventional dice called Zocchi dice, or funky dice, alongside with the traditional D&D dice.
 |
| Figure 4: Zochi dice: d3, d5, d7, d14, d16, d24 and d30. |
DCC uses the dice chain
d3 > d4 > d5 > d6 > d7 > d8 > d10 > d12 > d14 > d16 > d20 > d24 > d30 > d100
to express advantage and disadvantage. Normal checks are rolled with the 1d20, whilst advantage and disadvantage climb or descend the dice chain by a number of steps depending of how advantageous or disadvantageous the roll is. For instance, a normal advantage is designed as a step up in the dice chain (1d16 vs DC), and a normal disadvantage is designed as a step down in the dice chain (1d24 vs DC). Advantageous and disadvantageous modifiers can be summed together, moving on the dice chain up (+1d) and down (-1d). For instance, a roll with two advantages (+2d) and one disadvantage (-1d) would be rolled with a 1d30 instead of the traditional 1d20.
 |
| Figure 5: Probability of success when rolling with the DCC's advantage and disadvantage rule. |
With DCC's dice chain rule for checks, the probability of success barely changes for low DCs, but it changes widely for higher DCs, as the maximum value of the die check changes above and below 20. It means that a character in advantage has the chance of succeeding for DCs that were normally impossible, whereas it makes it impossible to succeed vs some high DCs. Strategically, this makes advantage and disadvantage much more important in game. The players gain a lot, if they are creative for gaining advantage in combat and skill checks. If they are smart, they will try to figure out strategies to convince the DM to give them more advantage.
In combat, going up the dice chain decreases the chance of rolling critical failure, and increases the chance of getting critical success. Values of critical success are the top numbers of each die 20, 24, 30 and 100. Lower dice don't grant critical successes.
Unfortunately, the Zochi dice don't move with constant steps in the dice chain. There are steps of d(+1), d(+2), d(+4), and d(+6). The steps are also not very symmetric around the d20. Nevertheless, if you roll digital dice on the computer, you can always make your own dice chain. However, I always find rolling physical dice more fun.
Advantage and Disadvantage Rule Alternative
I've been thinking another way of doing advantage and disadvantage without the. Instead of moving on the dice chain, the roll is made by
1d20 +/- (1d4 or 1d8 or 1d12)
I am not showing the graph here, but the range becomes 2-to-24 (1d20 + 1d4) for a simple advantage, and -3-to-19 (1d20 - 1d4) for a simple disadvantage. The success probability chance is linear in the middle with +/-2.5, and decreasing at the ends. For example, in 1d20 + 1d4, there is 1-in-80 chance of rolling 2, but there is 1-in-20 of rolling a 7 or 15. This system produces a probability of success like the modifier graph (Fig. 2), but with rounded ends. It would be more symmetrical than the 5e's system.